Collaborative live-coding with GPU
So, I wanted to combine teaching GPU computing in Python with collaborative notebooks. I got the idea of combining Numba, that I started exploring here, with a notebook that I could use in class with collaborative editing. As I mentioned earlier, I wanted to try out Google Colaboratory with its Jupyter-like notebooks. Google Colaboratory actually offers GPU support in their runtime, so this looked like the perfect match.
Well, so far I have not been able to make it work. It seems that the CUDA toolkit is not installed in the runtime environment from the beginning, so I had to find a way to do that. I have tried two approaches so far:
- Use
pipto install Numba and then install the CUDA toolkit from NVIDIA’s repository usingapt. - Install Anaconda’s Miniconda installer and then use that to install Numba and the CUDA toolkit.
The good news: both approaches seem to work for installing the library/package. However, so far I cannot get any of it to run…
1. pip and apt
So this is what I have tried so far in a Google Colaboratory notebook.
First, installing Numba is straight-forward:
!pip install numba
Then I install CUDA from NVIDIA’s instructions. This works almost out of the box:
!wget http://developer.download.nvidia.com/compute/cuda/repos/ubuntu1604/x86_64/cuda-repo-ubuntu1604_9.1.85-1_amd64.deb !dpkg -i cuda-repo-ubuntu1604_9.1.85-1_amd64.deb
Then I had to install the dependency dirmngr as well:
!apt install dirmngr
…and then continuing from NVIDIA’s instructions:
!apt-key adv --fetch-keys http://developer.download.nvidia.com/compute/cuda/repos/ubuntu1604/x86_64/7fa2af80.pub !apt-get update !apt-get install cuda
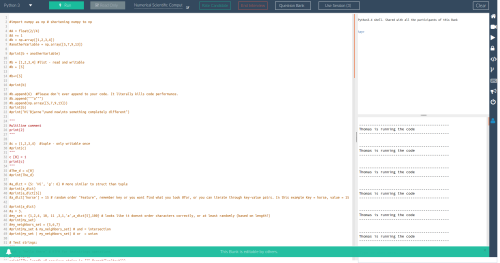
All of this went fine so far, but then I tried to run a Numba example:
import numpy as np
from numba import vectorize
@vectorize(['float32(float32, float32)'], target='cuda')
def Add(a, b):
return a + b
# Initialize arrays
N = 100000
A = np.ones(N, dtype=np.float32)
B = np.ones(A.shape, dtype=A.dtype)
C = np.empty_like(A, dtype=A.dtype)
# Add arrays on GPU
C = Add(A, B)
Unfortunately Numba throws an error and complains:
---------------------------------------------------------------------------
OSError Traceback (most recent call last)
/usr/local/lib/python3.6/dist-packages/numba/cuda/cudadrv/nvvm.py in __new__(cls)
110 try:
--> 111 inst.driver = open_cudalib('nvvm', ccc=True)
112 except OSError as e:
/usr/local/lib/python3.6/dist-packages/numba/cuda/cudadrv/libs.py in open_cudalib(lib, ccc)
47 if path is None:
---> 48 raise OSError('library %s not found' % lib)
49 if ccc:
OSError: library nvvm not found
It seems nvvm was supposed to be part of the CUDA toolkit, but it is nowhere to be found…
2. Anaconda
Then I decided to try using Anaconda instead since I know the CUDA toolkit is available here and straight-forward to install using the conda package manager. I started by downloading and installing Miniconda:
!wget https://repo.continuum.io/miniconda/Miniconda3-latest-Linux-x86_64.sh !bash Miniconda3-latest-Linux-x86_64.sh -b
This installed fine. Next, I decided to try installing the necessary packages in a conda environment:
!/content/miniconda3/bin/conda create -y -n cudaenv numba cudatoolkit
This worked as well – hooray! But: I cannot activate the cudaenv environment. Anaconda environments must be activated using the command source activate. But the bash command source is not available in collaboratory, so I am stuck here.
I have also tried to install Numba and CUDA directly in the default environment:
!/content/miniconda3/bin/conda install -y numba cudatoolkit
The installation works in this case as well, but I cannot seem to modify the path in the Colaboratory notebook to use Miniconda’s installed Python instead of the default system Python, so again I am stuck. I have tried prepending the path to Miniconda’s Python binary to both the system PATH variable as well as the PYTHONPATH variable via !export PATH…, but that does not seem to have any effect – I guess because we are already inside a notebook with a running Python interpreter.
Solution ideas are very welcome. I would love to get the Colaboratory notebook running with working Numba CUDA support, so I can use this to demonstrate GPU computing from Python in my course.
 Our next keynote speaker in line for the event is
Our next keynote speaker in line for the event is  Holger Rauhut is Professor for Mathematics and Head of Chair C for Mathematics (Analysis) at RWTH Aachen University. Professor Rauhut came to RWTH Aachen in 2013 from a position as Professor for Mathematics at the Hausdorff Center for Mathematics, University of Bonn since 2008.
Holger Rauhut is Professor for Mathematics and Head of Chair C for Mathematics (Analysis) at RWTH Aachen University. Professor Rauhut came to RWTH Aachen in 2013 from a position as Professor for Mathematics at the Hausdorff Center for Mathematics, University of Bonn since 2008. Florent Krzakala is Professor of Physics at École Normale Supérieure in Paris, France. Professor Krzakala came to ENS in 2013 from a position as Maître de conférence in ESPCI, Paris (Laboratoire de Physico-chimie Theorique) since 2004. Maître de conférence is a particular French academic designation that I am afraid I am going to have to ask my French colleagues to explain to me 😉
Florent Krzakala is Professor of Physics at École Normale Supérieure in Paris, France. Professor Krzakala came to ENS in 2013 from a position as Maître de conférence in ESPCI, Paris (Laboratoire de Physico-chimie Theorique) since 2004. Maître de conférence is a particular French academic designation that I am afraid I am going to have to ask my French colleagues to explain to me 😉 Our next speaker is Phil Schniter. Phil Schniter is Professsor in Electrical and Computer Engineering at Department of Electrical and Computer Engineering at Ohio State University, USA.
Our next speaker is Phil Schniter. Phil Schniter is Professsor in Electrical and Computer Engineering at Department of Electrical and Computer Engineering at Ohio State University, USA.